Ar gali žmogus išlaikyti 100 tonų krovinį, ranka suploti geležį, ar gali vaikas pasipriešinti stipruoliui? Taip gali. Pritaikius momentų dėsnį, žmogui galima suteikti pasakišką jėgą. Pats paprasčiausias pavyzdys - sverto veikimas. Svertas tai kietasis kūnas, kuris gali suktis apie įtvirtintą ašį arba turi atramos tašką.
         Jūs norite lazda pakelti akmenį. Tai pavyks, nors jo masė ir didesnė negu galite pakelti. Lazda padėta ant atramos , o atramos taškas - sukimosi centras. Kūną veikia du jėgos momentai: trukdantis - dėl akmens svorio įtakos ir stumianstis - dėl rankos veikimo. Ranka spaudžia vieną sverto galą jėga F₁, o akmuo - kitą sverto galą jėga F₂. Akemenį pakelsime, kai M₁ būs didesnis už M₂.
        Nulaikyti akmenį galima, kai M₁ = M₂, t.y. F₁·l ₁ = F₂· l₂. Iš čia gauname sverto taisyklę:

Svertas pusiausvyras yra tada, kai jį veikiančios jėgos atvirkščiai proporcingos jų pečiams.

        Sverto pusiausvyros taisyklė galioja ir tada, kai jį veikia ne dvi, o kelios ar keliolika jėgų. Pusiausvyros sąlyga ir šiuo atveju nustatoma pagal momentų taisyklę: jėgų momentų, veikiančių svertą prieš laikrodžio rodyklę, suma turi būti lygi jėgų momentų, veikiančių svertą pagal laikrodžio rodyklę, sumai.
         Ne vienas esame matę, kaip statybininkai naudodamiesi skridiniu, užmautu ant ašies ratuku, aukštyn susikelia reikalingus sunkesnius daiktus. Tačiau skridiniai gali būti nekilnojamieji ir kilnojamieji.
         Nekilnojamieji skridiniai tvirtinami aukščiau nei reikia pakelti krovinį. Prie vieno virvės galo pririšamas krovinys, o kitą traukiame žemyn.        Nekilnojamąjį skridinį galima laikyti lygiapečiu svertu. Lygios jėgos viena kitą atsveria.

Nekilnojamuoju skridiniu jėgos nelaimime, o tik pakeičiame jėgos veikimo kryptį

         Keliant krovinį kilnojamuoju skridiniu, kartu keliasi ir skridinys. Todėl jis ir vadinamas kilnojamuoju skridiniu. Kilnojamasis skridinys yra svertas, kurį jėgos veikia iš vienos atramos A pusės. Keliamo pasvaro svorio P petys lygus l₁ , kėlėjo jėgos F petys l₂. Pusiausvyros sąlyga: P · l₁ = F · l₂. Tačiau l₂ du kartus ilgesnis už l₁, tai F turi būti perpus mažesnis už P. O išmatavę virvės ir pasvaro nueitą kelią, matome, kad pasvaras pakilo perpus mažiau nei virvė.

Vadinasi, kilnojamuoju skridiniu laimime dvigubai jėgos, bet dvigubai pralaimime kelio.

Plokštuma sudaranti kampą su horizontu, vadinama nuožulniąja.

Jas dažnai naudoja sunkiems daiktams įridenti ar įstumti į sunkvežimį, o ne kelti tiesiai nuo žemės į sunkvežimį. Galima palyginti darbą reikalingą kroviniui užkelti vertikaliai į aukštį h: A = P · h ir atleikamą darbą, traukiant krovinį nuožulniąja plokštuma A = F · l.

Eksperimentiškai atlikus ir išmatavus veikusias jėgas ir nueitą kelią abiem atvejais gautume, kad atliktas darbas vienodas: P· h = F · l. Gauname:

Kroviniui pakelti nuožulniąja plokštuma reikia tiek kartų mažiau jėgos, kiek kartų plokštumos ilgis didesnis už jos aukštį

        Įrankiai daro žmogų stipresniu. Bet tai dar nereiškia, kad jais žmogus, įdėjęs mažai darbo, gaus didesnį darbą. Energijos tvermės dėsnis įtikina, jog neįmanoma laimėti arba, t.y. sukurti darbą iš "nieko". Gautasis darbas negali būti didesnis už įdėtąjį. Priešingai, naudojantis įrankiais, atliktas darbas visada bus mažesnis už įdėtąjį, nes dėl trinties neįmanoma išvengti energijos nuostolių. Idealiu atveju šie darbai bus lygūs.
         Sakykime jėgų veikiami taškai nueina kelius s₁ ir s₂. Tuomet darbų lygybės sąlyga: F₁· s₁ = F₂· s₂. Veikdami jėga jėga F₁, svertiniu įrankiu nugalėsime žymiai didesnę jėgą F₂. Tačiau rankos poslinkis s₁ bus tiek kartų didesnis už s₂, kiek kartų raumenų jėga F₁ mažesnė už F₂.

Vadinasi kiek kartų laimime jėgos, tiek kartų pralaimime kelio. Tai vadinama auksinė mechanikos taisyklė.

        Ši taisyklė tinka visiems paprastiesiems mechanizmams ir ne vienu iš jų nelaimime darbo.
        Kalbant apie atliktą darbą, neatsižvelgėme į trintį ir šių prietaisų svorį. Pavadinę mechanizmo atliktą darbą kroviniui pakelti naudinguoju darbu, veikiančios jėgos darbą - visu darbu ir juos palyginę, pamatysime, kad naudingas darbas A_n visada mažesnis už visą A_v. Dalis darbo sunaudojama įveikti trinčiai mechanizme ir jo detalėms kilnoti.

Naudingojo ir viso atlikto darbo santykis vadinamas mechanizmo ar mašinos naudingumo koeficientu

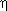
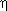
        Naudingumo koeficientas visada yra mažesnis už vienetą (0< <1), bet galima išreikšti ir procentais (0%< <100%).